
Important Note
This question is a part of the official practice exams (mocks). Please go through the following solution only if you already encountered this question and are looking for a solution. If you are yet to come across this question in your GMAT prep, it may be better to skip this article, as you may get this question in one of your practice exams in the future.
Question
In a marketing survey, 60 people were asked to rank three flavors of ice cream, chocolate, vanilla, and strawberry, in order of their preference. All 60 people responded, and no two flavors were ranked equally by any of the people surveyed. If 3/5 of the people ranked vanilla last, 1/10 of them ranked vanilla before chocolate, and 1/3 of them ranked vanilla before strawberry, how many people ranked vanilla first?
Given this is an official question, because of copyright, the complete question cannot be shown here. The question can be accessed at GMATClub by searching using the question text online.
Solution
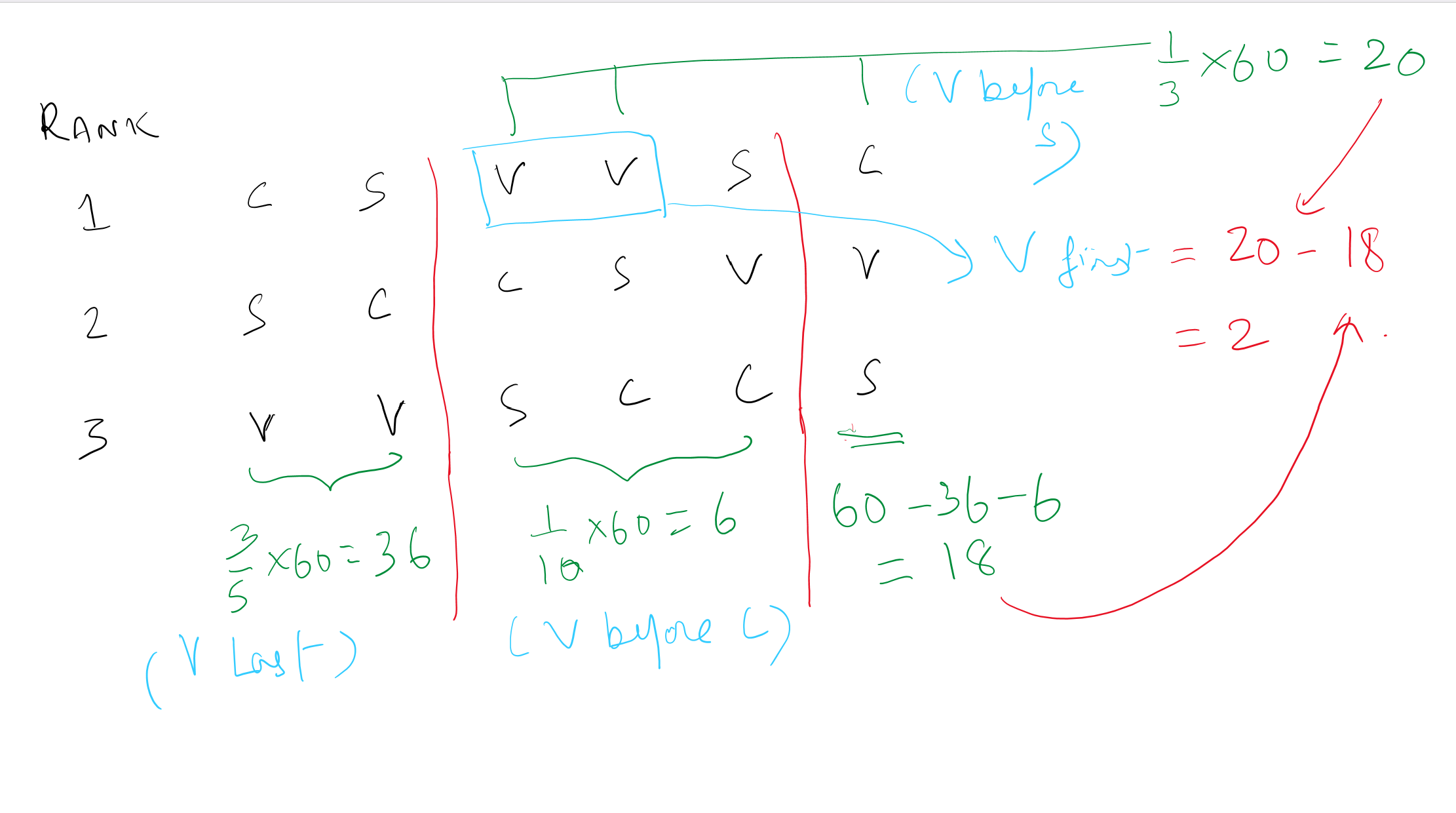
The answer: 2.
Sometimes, we have a mental block against listing out all the possible scenarios because our mind is telling us that it is a time-taking activity, and we should solve without having to list out every scenario.
One learning from this question is that if the number of possible scenarios is small (as in this case – there are only six possible ranking sequences), it may be easier to solve the question if one lists out the possibilities and works with that knowledge.
When the number of possibilities/scenarios is small, don’t shy away from listing those out if need be.
Another approach to solve this question:
The above is a visual + math-y way of solving this question. But GMAT quant questions are awesome in the fact that there are often multiple ways to solve them. And by spending time with the questions and good explanations, we can expand our thinking to multiple approaches – it will help come exam time!
For instance, in this question ->
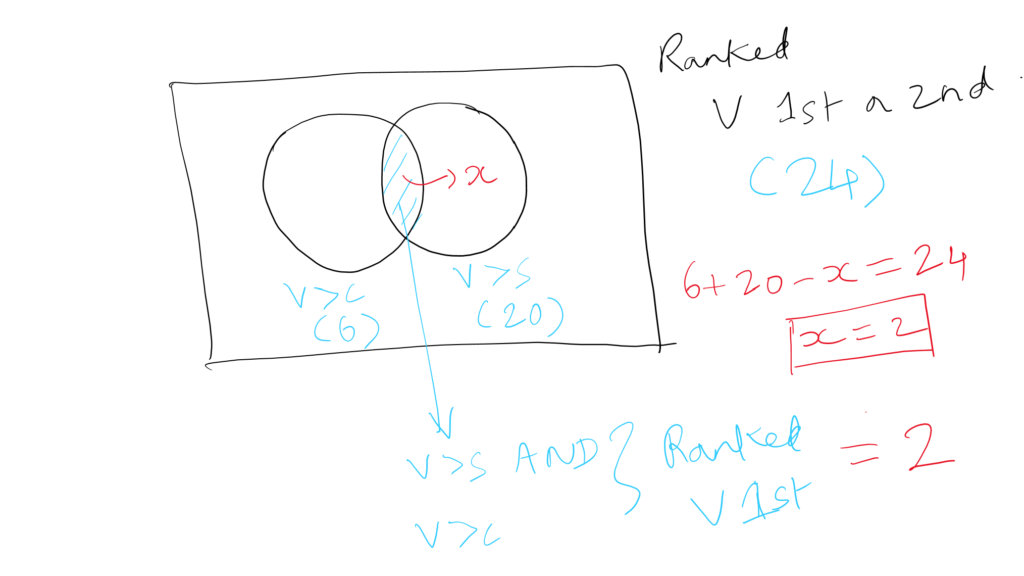
1) 36 people ranked vanilla last. This means 60 – 36 = 24 people exist who ranked vanilla either 1st or 2nd. What we are looking for is a subset of these 24 people (just the ones who ranked vanilla 1st).
2) Only 6 people ranked vanilla above chocolate (so 54 people ranked chocolate over vanilla). The 54 people who ranked chocolate over vanilla cannot have ranked vanilla first. What this means is that the number of people who ranked vanilla first cannot be more than 6. You can reject choices C, D, and E right here :).
3) Out of those 24 people who ranked vanilla above at least one other flavor (chocolate or strawberry or both) ->
-> 6 ranked vanilla over chocolate
-> 20 ranked vanilla over strawberry
-> How many ranked vanilla over both?
20 + 6 – 24 = 2.
Hope this helps!
Harsha
