
Important Note
This question is a part of the Focus Edition practice exams (mocks). Please go through the following solution only if you already encountered this question and are looking for a solution. If you are yet to come across this question in your GMAT prep, it may be better to skip this article, as you may get this question in one of your practice exams in the future.
Question
The chart above shows political and geographic data on a certain legislative committee of 20 members, each of whom belongs to 1 of 2 political parties and lives in 1 of 4 regions. How many subcommittees of this legislative committee are possible that contain exactly 1 member from each of the 4 regions and the same number of members from each of the 2 political parties?
Given this is an official question, because of copyright, the complete question cannot be shown here. The question can be accessed at GMATClub by searching using the question text online.
Solution
Brief Solution
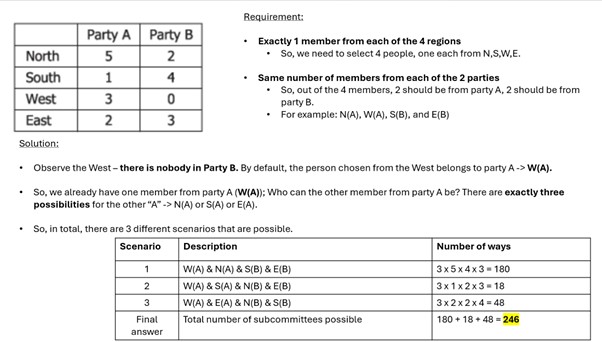
Detailed Solution
The above explanation should suffice if you have some conceptual familiarity with combinations. But if you are someone who needs a little more support, perhaps a detailed explanation of how the above calculation was done, do not worry – I got you covered. Read on!
Conditions that must be met:
• Exactly 1 member from each of the 4 regions
• So, we need to select exactly 4 people, one each from N, S, W, and E.
• Same number of members from each of the 2 parties
• So, out of the 4 members to be selected, exactly 2 should be from party A and exactly 2 should be from party B.
• For example: N(A), W(A), S(B), and E(B). This is an example that meets the conditions. In this case, the North and West members are from party A whereas the South and East members are from party B.
Finding the number of subcommittees possible that meet the above conditions:
Observe the given chart. Specifically, observe the West – there is nobody in Party B from the West. By default, the person chosen from the West has to belong to party A (say – W(A)).
So, we already have one member from party A fixed (W(A)). Great. We need exactly one more from party A and the other two from party B.
Who can the other member from party A be?
There are exactly three possibilities for the other member from party A -> N(A) or S(A) or E(A). in each of these cases, the remaining two members must be picked from party B to meet the criteria, as we have seen.
So, in total, there are 3 different scenarios that we need to consider to find the number of subcommittees meeting the given conditions.
|
Scenario |
Description |
|
1 |
W(A) and N(A) and S(B) and E(B) |
|
2 |
W(A) and S(A) and N(B) and E(B) |
|
3 |
W(A) and E(A) and N(B) and S(B) |
Observe the chart containing the number of members given in the question again. Now, let’s understand how to calculate what is needed!
1. In how many ways can a member from the West belonging to party A be selected?
a. 3 (i.e., 3C1).
2. Similarly, a member from the East belonging to party A can be selected in 2 ways.
3. In how many ways can two members be selected, W(A) and N(A)?
a. 3 x 5 (AND implies multiplication)
4. Continuing this way, in how many ways can a subcommittee adhering to situation 1 be selected?
a. W(A) and N(A) and S(B) and E(B) -> 3 x 5 x 4 x 3 = 180 ways
5. Similarly, we can calculate the number of ways in which situations 2 and 3 can occur too.
6. Now, remember that in reality, only one out of the 3 situations will play out. It is situation 1 OR situation 2 OR situation 3.
a. Hence, the total number of possible subcommittees will be the SUM of the total number of subcommittees adhering to each of the 3 situations. (OR implies addition)
Thus,
|
Scenario |
Description |
Number of ways |
|
1 |
W(A) and N(A) and S(B) and E(B) |
3 x 5 x 4 x 3 = 180 |
|
2 |
W(A) and S(A) and N(B) and E(B) |
3 x 1 x 2 x 3 = 18 |
|
3 |
W(A) and E(A) and N(B) and S(B) |
3 x 2 x 2 x 4 = 48 |
|
Final answer |
Total number of subcommittees possible |
180 + 18 + 48 = 246 |
The answer to the question: 246. (Choice D).
Hope this helps.
Harsha
